Hey everyone! It's been more than a month since the launch of Super Space Smugglers for the TK Game Jam and I have a confession to make.

I lied to you.

You were under the impression that you were playing a game with state-of-the-art accurate physics simulations - but that couldn't be further from the truth.

In Super Space Smugglers in fact - you were all flying in a deception powered orbital system. The deception lies mostly in how the planets move. The player's ship is actually pretty accurately simulated with "N-body physics" - that is at every frame we apply an appropriate gravitational force based on the mass and distance to every celestial body in the game.

The planets however are simply clockwork - each planet moves on a strictly circular orbit and their positions over time are calculated using sin and cos with some arbitrarily selected orbital period.

But it's time to change that!

You will be happy to learn that we're continuing to develop this project and the first issue on the docket is to implement physically accurate orbital mechanics.

In this post you'll get a glimpse into how things move around in space (unless affected by a force) and how we're implementing it in our game.

A brief history lesson

A few centuries ago a man named Johannes Kepler broke away from the chains of antiquity and declared that orbits don't have to be perfect circles! Through meticulous (stolen borrowed) observations of the motions of the planets in our Solar System he came to a few revolutionary conclusions. And after many years of calculations, during which he made many mistakes that miraculously ended up cancelling themselves out, Kepler gave birth to the field of Astrodynamics, also known as Orbital Mechanics.

Kepler gave us laws of planetary motion. I won't bore you with the details but they boil down to the following:

1. Orbits are ellipses
2. Planets move in a non-uniform speed on these orbits
3. An orbital period can be calculated pretty easily given good measurements

And just to praise the man a little bit more - all of this happened before the discovery of gravity, Isaac Newton would release his Principia 57 years after Kepler's death.

What about the game?

Ok, that's all very nice and interesting (at least to me) - but what about the game? How can we translate Kepler's laws into code that simulates orbits?

The first step is to figure out what data do we need to represent an orbit.

One way is to simply measure an object in space. With just 2 measurements we can infer its position and velocity. Which gives us six numbers - the xyz components of both vectors.

There is however a different way and it's a way that Kepler would have used when measuring planets in orbit. Kepler would also use six numbers but they would be:

1. Semi major axis
2. Eccentricity
3. Inclination
4. Right ascension of the ascending node
5. Argument of periapsis
6. True anomaly

They sound very cryptic for now but as you continue reading you'll find that they're actually quite simple to understand geometrically.

The first 2 parameters simply describe the shape of an ellipse. Imagine you have a circle and draw 2 lines through the center such that they are perpendicular to one another. 

These lines are the diameters of the circle and their halves are the radii. Now stretch out this circle into an ellipse along one of these lines. 

We call the longer line that major axis of the ellipse. Half of this line would therefore be the semi major axis. Eccentricity tells us how much a given orbit is an ellipse. Let's not bother with the formula for now - let's just understand the following. An orbit with eccentricity equal to zero is perfectly circular - in practice such orbits don't exist and are also extremely annoying to calculate. An orbit with an eccentricity between 0 and 1 is an ellipse and the closer to 1 the more stretched out this ellipse is.

There are also two more kinds of orbits defined by their eccentricity. An orbit of an object that is not fully captured by the gravitational forces of the body its orbiting. These objects are following a parabolic (for eccentricity equal to 1) or hyperbolic (for eccentricity higher than 1) trajectories. An example of such object in real life could be the ʻOumuamua - a recent visitor to our Solar System. It's orbit has an eccentricity of 1.20113 and it zipped passed our Sun and all the planets and is now well on it's way out of our system, never to return.

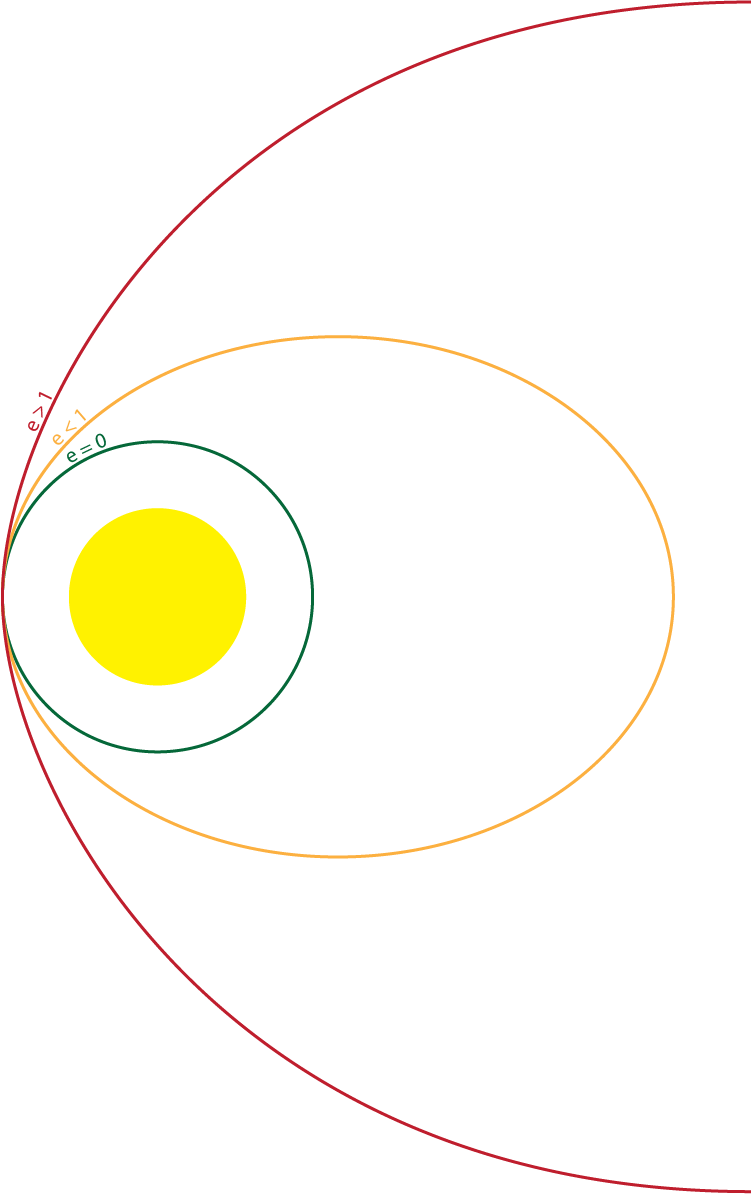
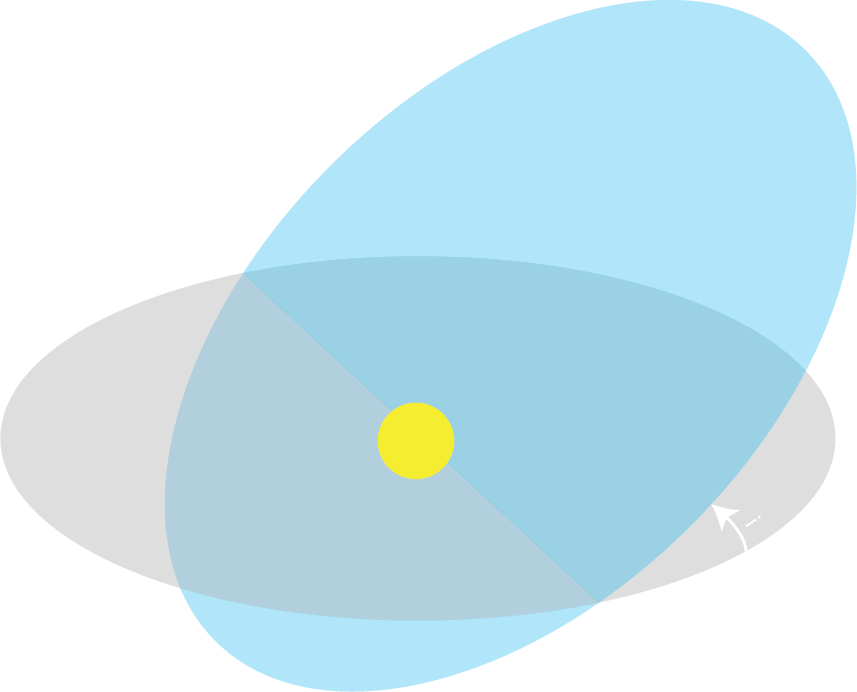
Now, we've established that in reality no orbit is perfectly circular. No orbit is also perfectly aligned with the equatorial plane of the Sun - i.e. the plane that cuts that Sun in half and is perpendicular to its axis of rotation. All planets (and other celestial objects) have an inclination. In order to be able to determine how inclined an orbit is we must first figure out the axis along which this rotation occurs. For that we use 2 points on the orbit which we call the Ascending and Descending Node. We can find these points pretty easily by finding the intersection of the ellipse of the orbit with the equatorial plane. As the names suggest the Ascending Node is the point at which the celestial object rises above the equatorial plane. While the Descending Node is the point at which it descends below it. The two points give us a line - also called a Node line - which we can rotate the orbit around. And the angle by which the orbit is rotated is the inclination.

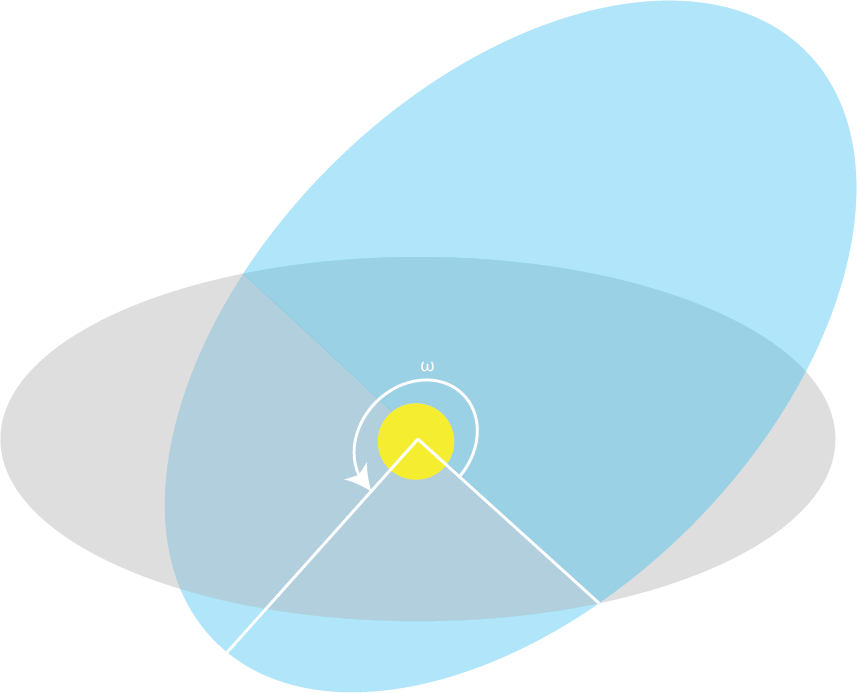
The orbit can then be rotated along two different axis. We can obtain the first axis with the following steps. Let's take a flat non-inclined orbit and let's draw a line that is perpendicular to the plane of this orbit and anchored at the central body (i.e. the Sun). We call the rotation along this axis the argument of periapsis - denoted by ω - and it's measured as the angle between the vector towards the ascending node and a vector pointing to the periapsis. 

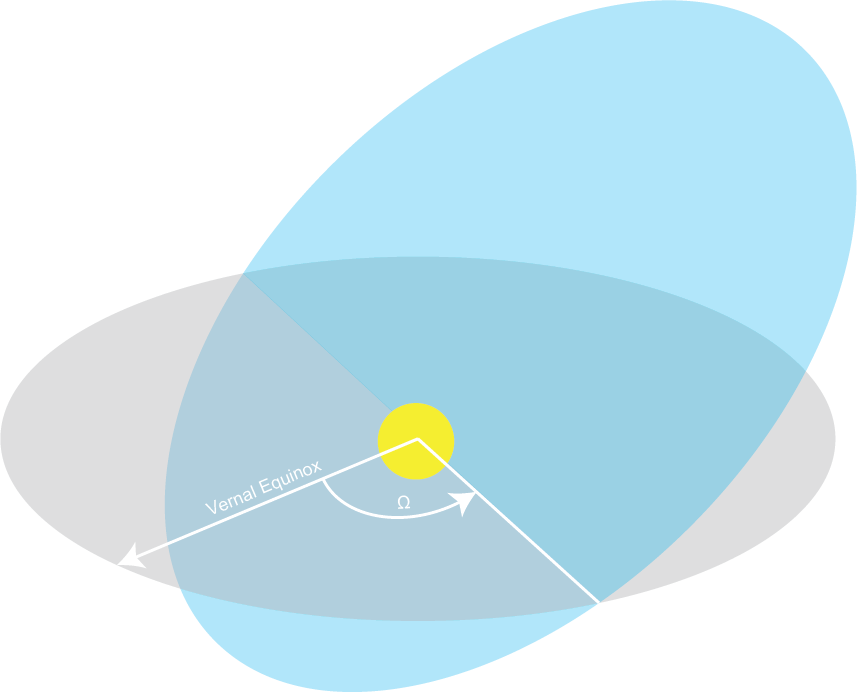
The second rotation is much simpler as we simply rotate around a line perpendicular to the equatorial plane anchored at the central body. The rotation is measured from some arbitrary reference vector - often the vernal equinox - and to the vector pointing to the ascending node - we call this angle the longitude of the ascending node - typically denoted by Ω.

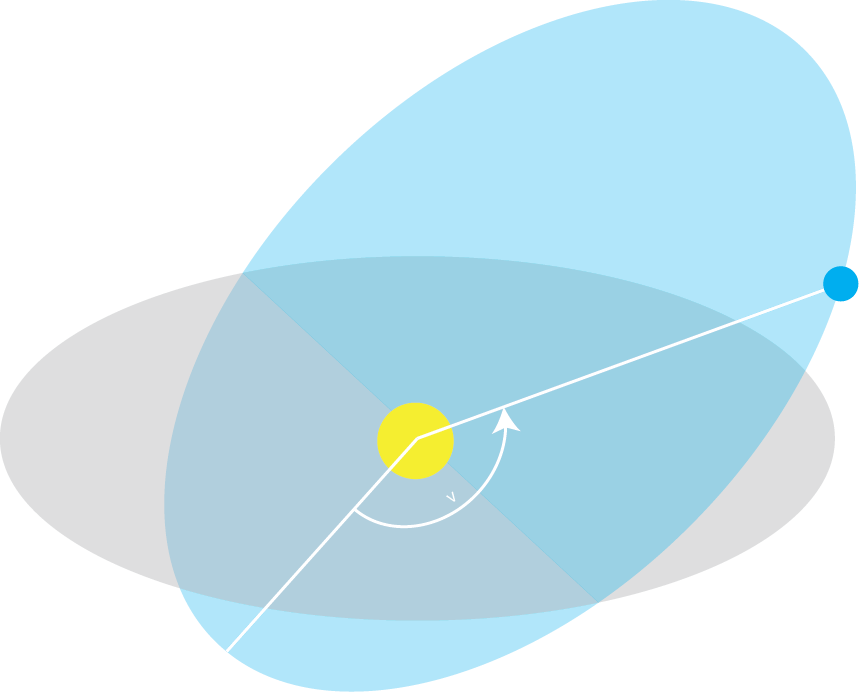
With these three rotations our orbit is now aligned in three dimensional space. What remains is to figure out where on the orbit ellipse is the body located. This is given to us by the True Anomaly. Anomaly in this context is simply an old-timey name for an angle. The true anomaly is an angle - typically denoted by v - between the direction to the periapsis and the current position of the orbiting body, where both directions are take from point of view of the central body.

Oof, that was a lot. I think that's enough for one post.  Next time I'll have some actual code samples for you and a maybe even some juicy gifs.

Hope you learned something and let me know in the comments if you'd like to see more posts on these subjects. And remember to follow us for more updates on this project!

Fly safe!